Leading Streak Today
Your Streak Today
Leading Streak Today
Your Streak Today
6⁄5 is an improper fraction.
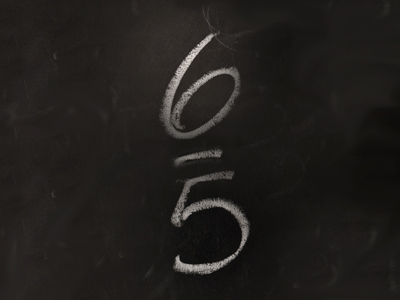
Fractions (Year 5)
In KS2 Maths, as you go into Year Five, you'll learn more about fractions. Fractions are like puzzle pieces of numbers less than one. You'll discover values, numerators, denominators, and even mixed numbers and decimals.
Imagine you have 2.5 sweets. In fractions, that's 21⁄2 or 5⁄2. The first one is a mixed number (2 whole sweets and a half), and the second is an improper fraction (more on the top than the bottom). Proper fractions have smaller tops!
Curious to learn more? Visit our 'Help With Fractions' blog for fun tips on understanding these maths adventures!
Click to See How Quizzes Help Learning
1 .
What would 6⁄4 be when converted to a mixed number?
41⁄2
11⁄2
11⁄4
21⁄4
A mixed number is where there is a mix of a whole number and a fraction
2 .
Which fraction is less than 1⁄2?
51⁄100
7⁄12
5⁄9
7⁄15
2 x 7 = 14 so 7⁄15 is slightly less than half
3 .
What type of fraction is 6⁄5?
Mixed fraction
Equivalent fraction
Improper fraction
Unsuitable fraction
An improper fraction has a top number more than the bottom number
4 .
Which fraction is one ninth?
1⁄8
1⁄9
1⁄6
1⁄12
1⁄9 is the same as 1 ÷ 9
5 .
Which fraction is 25⁄100 equivalent to?
1⁄4
1⁄8
1⁄2
1⁄5
100 ÷ 25 = 4
6 .
Which of these fractions is not equivalent to 1⁄3?
2⁄6
4⁄12
3⁄9
2⁄10
2⁄10 is the same as 1⁄5
7 .
What would 31⁄4 be when converted to an improper fraction?
11⁄4
5⁄8
13⁄4
13⁄3
There are 4⁄4 in 1 one so 3 ones = 12⁄4
8 .
Which of these is a proper fraction?
9⁄12
7⁄6
4⁄3
12⁄9
A proper fraction has a top number less than the bottom number
9 .
Which is the largest of these fractions?
3⁄9
9⁄12
35⁄100
1⁄2
9⁄12 is larger because 9 is closer to 12 than 3 is to 9, 35 is to 100 and 1 is to 2
10 .
Which fraction is more than 1⁄4?
2⁄8
3⁄12
6⁄20
25⁄100
5⁄20 is equivalent to 1⁄4 so 6⁄20 is more
**Unlimited Quizzes Await You! 🚀**
Hey there, quiz champ! 🌟 You've already tackled today's free questions.
Ready for more?
Ready for more?
🔓 Unlock UNLIMITED Quizzes and challenge yourself every day. But that's
not all...
not all...
🔥 As a Subscriber you can join our thrilling "Daily Streak" against other
quizzers. Try to win a coveted spot on our Hall of Fame Page.
quizzers. Try to win a coveted spot on our Hall of Fame Page.
Don't miss out! Join us now and keep the fun rolling. 🎉
**Unlimited Quizzes Await You! 🚀**
Hey there, quiz champ! 🌟 You've already tackled today's free questions. Ready for more?
🔓 Unlock UNLIMITED Quizzes and challenge yourself every day. But that's not all...
🔥 As a Subscriber you can join our thrilling "Daily Streak" against other quizzers. Try to win a coveted spot on our Hall of Fame Page.
Don't miss out! Join us now and keep the fun rolling. 🎉
Here To Help
Our Social Circles
© Copyright 2016-2024 - Education Quizzes
Work Innovate Ltd - Design | Development |
Marketing
