UKUK USUSIndiaIndia
Progress you can see
Parents Students Tutors Teachers QuizMaster (New)
Join Us
UKUK USUSIndiaIndia
Join Us
KS1 (Age 5-7)KS2 (Age 7-11)11 Plus (Age 7-11)KS3 (Age 11-14)GCSE (Age 14-17)PSHEA.I.ESLSpanishSpecialistGames
Lucy
Ask the AI Tutor
Need help with Fractions (Year 5)? Ask our AI Tutor!
Lucy AI Tutor - Lucy
Connecting with Tutor...
Please wait while we establish connection
Lucy
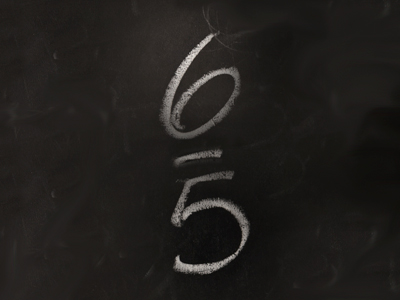
Hi! I'm Lucy, your AI tutor. How can I help you with Fractions (Year 5) today?
now
0/50 words
  1. Home
  2. KS2
  3. Maths
  4. Fractions (Year 5)
Fractions (Year 5)
6⁄5 is an improper fraction.

Fractions (Year 5)

Year 5 pupils explore fractions in more depth. They compare, order, and convert fractions, and practise applying them to solve both mathematical problems and real-world challenges.

Explore the Topic →
(quiz starts below)

Fascinating Fact:

The world record for the men’s marathon was beaten by less than one fifth of a minute, which is under 12 seconds.

In KS2 Maths, Year 5 pupils learn how fractions link to decimals and percentages. They work with improper fractions and mixed numbers, and practise using fractions to solve practical problems.

Key Terms

  • Improper Fraction: A fraction where the numerator is greater than the denominator, such as 7/4.
  • Mixed Number: A whole number combined with a fraction, like 2 3/5.
  • Percentage: A way of expressing a fraction out of 100, such as 50% meaning half.

Frequently Asked Questions (Click to see answers)

What are improper fractions in Year 5 Maths?

An improper fraction is when the top number is larger than the bottom, like 9/4. Pupils learn to convert these into mixed numbers.

How do Year 5 pupils convert fractions to decimals?

Pupils divide the numerator by the denominator. For example, 1/4 equals 0.25 as a decimal.

Why do we learn fractions in Year 5?

Fractions are used in real life for cooking, measuring, sharing, and understanding percentages. They help link whole numbers with decimals and percentages.

Try These Related Quizzes

1 .
Which of these is a proper fraction?
9⁄12
7⁄6
4⁄3
12⁄9
A proper fraction has a top number less than the bottom number
2 .
What would 31⁄4 be when converted to an improper fraction?
11⁄4
5⁄8
13⁄4
13⁄3
There are 4?4 in 1 one so 3 ones = 12?4
3 .
What type of fraction is 6⁄5?
Mixed fraction
Equivalent fraction
Improper fraction
Unsuitable fraction
An improper fraction has a top number more than the bottom number
4 .
Which fraction is one ninth?
1⁄8
1⁄9
1⁄6
1⁄12
1?9 is the same as 1 ÷ 9
5 .
Which fraction is 25⁄100 equivalent to?
1⁄4
1⁄8
1⁄2
1⁄5
100 ÷ 25 = 4
6 .
Which fraction is less than 1⁄2?
51⁄100
7⁄12
5⁄9
7⁄15
2 x 7 = 14 so 7?15 is slightly less than half
7 .
What would 6⁄4 be when converted to a mixed number?
41⁄2
11⁄2
11⁄4
21⁄4
A mixed number is where there is a mix of a whole number and a fraction
8 .
Which of these fractions is not equivalent to 1⁄3?
2⁄6
4⁄12
3⁄9
2⁄10
2?10 is the same as 1?5
9 .
Which is the largest of these fractions?
3⁄9
9⁄12
35⁄100
1⁄2
9?12 is larger because 9 is closer to 12 than 3 is to 9, 35 is to 100 and 1 is to 2
10 .
Which fraction is more than 1⁄4?
2⁄8
3⁄12
6⁄20
25⁄100
5?20 is equivalent to 1?4 so 6?20 is more
You can find more about this topic by visiting BBC Bitesize - Fractions

Author:  Amanda Swift (Primary School Teacher & Educational Content Developer)
Maths Play this quiz again

Here to Help

Contact Us
FAQs
Your Account

Resources

Parents Knowledge Bank Blog Links and Resources Quiz List and Sitemap Colour Filters Safe AI Survey Results

About

Our Team Testimonials Parent Reviews Terms and Conditions Privacy Policy

© Copyright 2016-2026 - Education Quizzes
Work Innovate Ltd - Design | Development | Marketing

We use cookies to enhance your experience on our website.

To comply with the e-Privacy directive, we need your consent - I agree - No thanks - Learn more